[알고리즘] 에라토스테네스의 체
[알고리즘] 에라토스테네스의 체
고대 그리스의 수학자이자 지리학자인 에라토스테네스가 고안한 소수를 찾는 방법으로 2를 제외한 2의 배수, 3을 제외한 3의 배수, 5를 제외한 5의 배수의 순서로 수를 지워나가 끝에 남는 수가 소수이다. 마치 체로 치듯이 걸러낸다고 하여 '에라토스테네스의 체' 라고 불린다. 이는 자연수 N에 대해서 그 이하의 수 중에서 소수를 찾는 가장 빠른 방법이다.
방법
- 1부터 N까지 소수를 구하고자 하는 구간의 모든 수를 쭉 나열한다.
- 우선 소수도, 합성수도 아닌 유일한 자연수 1을 제거한다.
- 남은 수 가운데 가장 작은 수를 제외한 배수를 모두 지운다.
- 3번 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.
위의 2번 과정을 조금 더 풀어서 흐름이 어떻게 진행되는지 살펴보자.
1. 남은 수 중 가장 작은 수 2를 제외한 2의 배수를 모두 제거한다.
2. 남은 수 중 가장 작은 수 3을 제외한 3의 배수를 모두 제거한다.
3. 남은 수 중 가장 작은 수 5를 제외한 5의 배수를 모두 제거한다.
4.
5. ....
이때 4의 배수는 2의 배수에서 걸러지게 된다.
위의 과정을 반복하면 구하는 구간의 모든 소수가 남게 된다.
그림을 이용해서 흐름을 살펴보자. 1부터 100까지의 소수를 찾아보자,
1. 1~100까지의 숫자를 나열한다.

2. 소수도 합성수도 아닌 1을 제거한다.
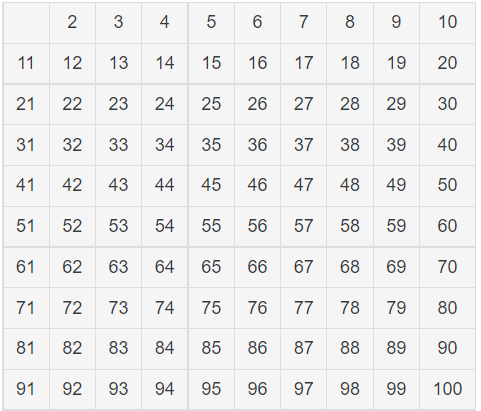
3. 남은 수 중에서 가장 작은 수 2를 제외한 2의 배수를 제거한다.
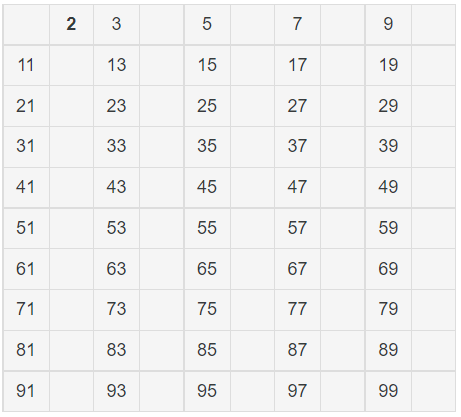
4. 남은 수 중에서 가장 작은 수 3을 제외한 3의 배수를 제거한다.
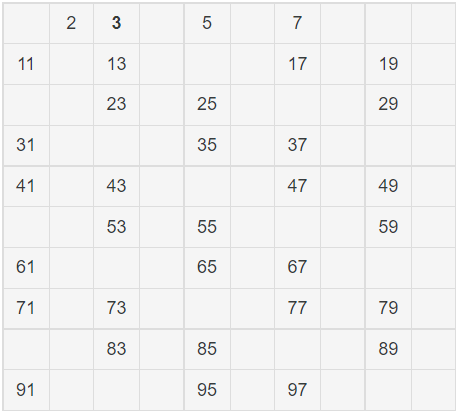
앞서서 설명했듯이 4는 소수가 아니다. 2의 배수에서 지워졌으므로!!
5. 남은 수 중에서 가장 작은 수 5를 제외한 5의 배수를 제거한다.

6. 남은 수 중에서 가장 작은 수 7을 제외한 7의 배수를 제거한다.

다음으로 8의 배수는 2의 배수에서 지워졌다. 9의 배수 또한 3의 배수에서 지워졌고 10의 배수도 2의 배수에서 이미 지워졌다. 그 이상의 수에 대해서는 살펴볼 필요가 없다.!! 그 이유는 소수 판정법에서 기술하였다. 11 > $\sqrt{100}$ 이므로 그 이후의 값은 지울 필요가 없다.
구현
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
public class prime {
public static void main(String args[]) {
// True : 소수가 X
int N = 100;
boolean[] check = new boolean[N+1];
check[0] = check[1] = true; // 0, 1은 소수가 아니므로 True를 넣어준다.
// 남은 수를 찾는 반복문.
for (int i=2; i <= Math.sqrt(100); i++) {
if (check[i] == true) {
continue; // 이미 지워진 수인 경우 건너 뛴다.
}
// 가장 작은 수를 제외하고 배수를 제거한다.
for (int j=i+i; j<=100; j+=i) {
check[j] = true;
}
}
for (int i=1; i<=100; i++) {
if (check[i] == false) {
System.out.print(i+" ");
}
}
}
}
|
정리
지금까지 에라토스테네스의 체를 이용해서 1부터 100까지 구간의 소수를 모두 구하는 방법과 구현 방법을 살펴보았다. 아직까지는 특정한 범위가 주어지고 그 범위 내에서 소수를 구하는 방법 중 에라토스테네스의 체보다 빠른 방법은 없다고 한다. 다시 한번 말하지만 "특정 구간 내에서 소수를 판정" 하는 데에는 매우 효과적이지 특정 수가 소수냐?! 라고 한다면 이보다 빠른 방법은 넘쳐 난다. 마지막으로 알고리즘 문제 풀이에 있어서 시간 복잡도를 고려한 후, 시간 내에 풀이가 불가능하거나 특정 범위의 소수를 활용하는 문제라면 적극적으로 에라토스테네스의 체를 활용해 볼 것을 권한다.
참고자료
댓글
이 글 공유하기
다른 글
-
[알고리즘] 소수 판별법
[알고리즘] 소수 판별법
2021.09.13 -
[탐색 알고리즘] lower_bound, upper_bound
[탐색 알고리즘] lower_bound, upper_bound
2020.07.18