[Python] 비트 연산
[Python] 비트 연산
Python3 비트 연산이 C/C++과는 조금 차이가 있는 것 같아서 비트 연산자에 대해서 다루어 보려고 한다.
다음과 같은 명령문이 있을 때 출력 결과를 살펴보도록 하자.
>>> bin(0b0101 ^ ~0b1100)
'-0b1010'
반환 값은 문자열이며 bin 함수를 통해서 2진수로 출력되었다. 또한 앞에 - 부호가 들어간 것을 알 수 있다. 크기는 10이다. 나는 처음 결과를 생각하기를 ~0b1100 은 0b0011이 되겠거니 생각을 해서 (0b0101 ^ 0b0011) XOR 연산 결과 '0b0110' 라고 단순히 생각을 했다. 보기와 다르게 결과는 그렇지 않다. 그렇다면 어디가 잘못된 것일까? ~연산자를 이해하기 위해서는 2의 보수를 이해하고 있어야 한다. 잠시 다음 표를 살펴보자.
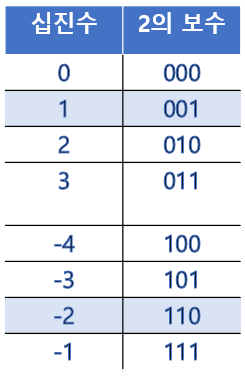
2의 보수는 컴퓨터가 음수를 저장하기 위한 방법 중 하나이다. 위의 3비트 정수의 예를 살펴보자. 3비트는 000 ~ 111로 8개를 표현할 수 있다. 양수만 저장 한다면 0 ~ 7까지 표현할 수 있고 음수까지 포함한다면 위의 테이블에서 알수 있듯이 -4 ~ 3 까지 정수를 표현 할 수 있다. 위의 테이블에서 음수의 2의 보수 표현을 보면 앞에 1xx로 시작하는 것을 알 수 있다. 맨 앞에 비트를 최상위 비트 즉 부호 비트라고 표현하기도 한다. 위에서 1과 -2의 십진수 및 2의 보수의 해당하는 칸을 보자. 001을 ~ (NOT) 연산을 취하면 (0 -> 1, 1 -> 0) 1은 -2가 되는 것을 알 수 있다. 왜 이 값이 나오는지는 이해했을 거라 생각한다.
~ 연산자 (NOT)를 알아보자.
>>> bin(~0b1100)
'-0b1101'
>>> ~ 12
-13
>>> ~ 3
-4
>>> ~ 0
-1
0b1100는 십진수 12 다. 여기에 ~ 연산자를 취했더니 -13 이라는 결과가 나온다. ~3 의 결과도 -4가 나왔다. 즉 x라는 값을 넣으면 ~x = -x -1 이라는 값이 나온다는 얘기다. 즉 2의보수를 취하고 그 값에서 1을 빼주는 연산을 해주면 된다. python3 에서는 음수를 보여줄 때는 양의 정수를 표현하는 방식과 동일하게 이진수로 표현하고 부호만 따로 앞에 표기를 한다. CPython은 임의 정밀도를 지원하기 때문에 내부적으로는 다소 복잡한 구조로 구현되어 있다. 비트 연산이 필요할 때만 2의 보수로 변환하는 작업을 진행한다.
다음의 예를 살펴보자
>>> bin(-10)
'-0b1010'
'0b1010' 은 크기는 10인 이진수이다. 하지만 앞에 - 부호가 있는 것을 알 수 있다. 이것이 위에서 설명한 Python3에서 음의 정수를 표현하는 방법이다. 2의 보수 값을 보여 주지 않는 다고 문제 될 것은 없다. 다른 비트의 연산 결과는 문제없으니 말이다.
문제가 되지 않음을 다음의 예시를 통해서 살펴보자.
>>> bin(5)
'0b101'
>>> bin(-4)
'-0b100'
>>> 5 & -4
4
>>> bin(0b0101 & 0b1100)
'0b100'
>>> bin(0b0101 & -0b100)
'0b100'
5 & -4 즉 5와 -4와의 & 연산하는 과정을 살펴볼 것이다. -4를 2진수로 표현하면 Python에서는 '-0b100' 이 된다. 하지만 -4를 4비트 음수로 표현하면 1100 이 될 것이다.(2의 보수법 표현) 그러나 어떻게 표현하든 비트 연산 결과는 동일함을 알 수 있다.
Python3 비트 연산에서 중요한 점을 꼽아 보면 다음의 항목과 같다.
1. 비트 연산자 NOT은 2의 보수에서 1을 뺀 것이고
2. 2의 보수 수학 연산은 비트 연산자 NOT(0을 1로 1을 0으로)에서 1을 더한 것이다.
예를 들어보면
1. 0b01011의 2의 보수 연산은 10100 + 1 = 10101이 된다.
2. 0b10101의 비트 연산자 NOT은 01011 - 1 = 01010이 된다.
마지막으로 Python3 에서는 자료형이 지정된 것이 아니기 때문에 C/C++에서 처럼 32비트, 64비트의 길이가 정해져 있는 것이 아니다. 따라서 0b101을 0000 0101로 또는 그 이상의 비트 길이로 해석하는 습관을 기르는 것이 좋다.
** 참고자료 **
파이썬 알고리즘 인터뷰